
In summary, when, there is no solution for a SSA configuration. Since the other given side length is and since, there is no solution.

This means that this third side can swing from the upper vertex in any way that connects this vertex and any point along the indefinitely sized base so that all three sides of the triangle are connected. The length of the third side length is also fixed, but neither angle adjacent to that side is known. The length of the base is unknown, denoted below by a dashed line. With the SSA configuration, there is a fixed angle connecting the base of the triangle and one of the adjacent sides. This configuration is commonly referred to as side-side-angle (SSA). According to triangle congruence postulates, two triangles cannot be proved congruent given these three elements. Given two adjacent side lengths and an angle opposite one of them, there is no definite completion of a triangle.
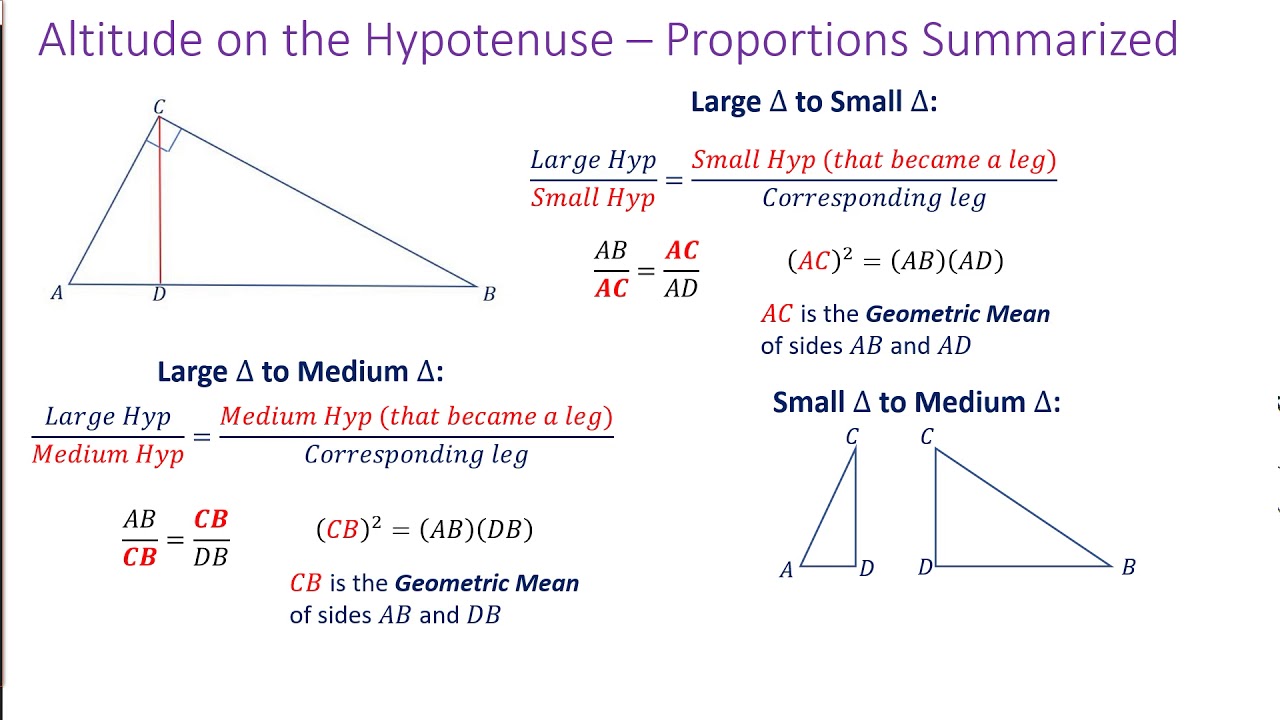
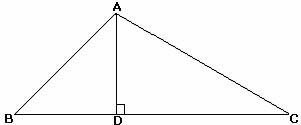
The point G is the centroid and point O is the orthocentre of ∆XYZ. Hence, ∆XYZ is the required triangle in which the medians XL, YK and ZU to the sides YZ, ZX and XY respectively intersect at G and altitudes XL, YM and ZN to the sides YZ, ZX and XY respectively intersect at O. With Q as centre and taking same radius, draw another arc that cut the previous arc at R. (xv) With P as centre and taking radius more than half of PQ, draw an arc. (xiv) With Z as centre and taking convenient radius, draw two arcs that intersect XY at P and Q. (xii) Draw the perpendicular bisector ST of the side XY that intersect XY at U. With F as centre and taking same radius, draw another arc that cut the previous arc at H. (x) With Z as centre and taking radius more than half of ZF, draw an arc. (ix) With Y as centre and taking convenient radius, draw two arcs that intersect ZX at Z and F. (vii) Draw the perpendicular bisector IJ of the side ZX that intersect ZX at K. With B as centre and taking same radius, draw another arc that cut the previous arc at C. (v) With A as centre and taking radius more than half of AB, draw an arc. (iv) With X as centre and taking convenient radius, draw two arcs that intersect YZ at A and B. (ii) Draw the perpendicular bisector DE of the side YZ that intersect YZ at L. Hence, ∆LMN is the required triangle in which the altitudes LI, MK and NJ to the sides MN, NL and ML respectively intersect at O. NJ is an altittude to the side ML produced. (xii) Join NC that intersect ML produced at J. With B as centre and taking same radius, draw another arc that intersect the previous arc at C. (xi) With A as centre and taking radius more than half of AB, draw an arc. (x) With N as centre and taking convenient radius, draw two arcs that intersect ML produced at A and B. (viii) Join MF that intersect NL produced at K. With E as centre and taking same radius, draw another arc that intersect the previous arc at F. (vii) With D as centre and taking radius more than half of DE, draw an arc. (vi) With M as centre and taking convenient radius, draw two arcs that intersect NL produced at D and E. With Q as centre and taking same radius, draw another arc that intersect the previous arc at R. (iii) With P as centre and taking radius more than half of PQ, draw an arc. (ii) With L as centre and taking convenient radius, draw two arcs that intersect MN at P and Q.


 0 kommentar(er)
0 kommentar(er)
